Nexus 7 で pi を計算する C4droid

結局今回は使わなかった Nexus 7 のアプリ、C4droid (C/C++ compiler)

n0n3m4 に付いている examples の中に、円周率を計算するサンプルコードがある。初期値２の p を、p*=((double)(((int)((i+2)/2))*2))/(((int)((i+1)/2))*2+1);　で百万回回している。その割に、実行結果は、Pi = 3.141591 ・・・小数点以下５桁までしか正しくない。しょぼい。何だこりゃ？

探しましたがな。
John Wallis(1616/11/23-1703/10/28) の Arithmetica Infinitorum (1656)に出てくる、いわゆるウォリス積

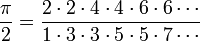
かっちょよく書くと

無限乗積だ！こりやぁ収束遅いわ。式はとっても美しいんだけど。ちょっと見てみる？

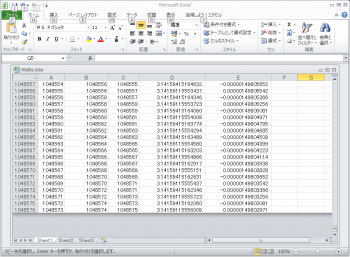
ここがexcel2010の底だよー。初めて見たでしょ。

Excel2010の行を使い尽くしてみた。超弩級に重たい。D列が近似値で、E列が真値との誤差。1,048,573回回しても小数点以下５桁までしか正しくないことが分かる。

何故、斯様な式を examples としたのか、全く意図がわからない。関孝和遺編「括要算法　貞」の、355/113 = 3.141592920・・・の方がよっぽどましだ。

ちなみに、おなじみ、Machinの公式。

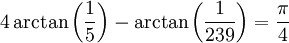
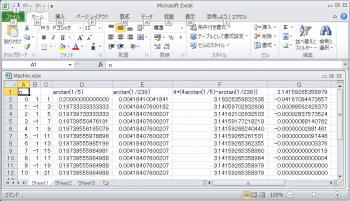
arctan をTaylor展開する。９回回して小数点以下１４桁をクリア。

いつもの「GNU/Linux上で円周率の計算をおこなう

」は、Gauss AGM。
初期値

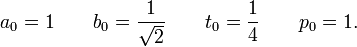
に対し

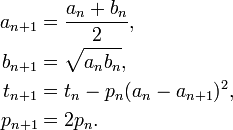
を行うと円周率の近似値は

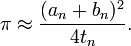
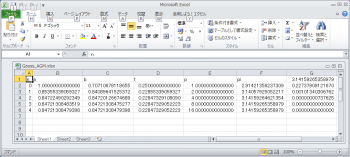
わずか３回のループで小数点以下14桁をクリア。実はこの時点で小数点以下18桁までクリアしている。このアルゴリズム、ｐn が曲者で、1024ループあたりで変数がオーバーフローしてしまう。浮動小数点で計算するのはこの辺が限度ということだ。

実際の多桁円周率計算は、多倍長整数で計算しなければならない。

最近のトレンドは、Chudnovsky algorithm だそうな。

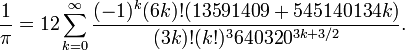
一項目、640320^(3/2) / 12 / 13591409 を電卓で計算すると、3.1415926535897342076684535915783・・・すげ！
二項目で27桁まで計算できちゃうみたい。

円周率を1億桁計算しました！ — その試行錯誤の詳しい経緯と結果

　プログラムモグモグ　itchynyさん

Machin と Gauss_AGM の xlsx ファイルを下に置いとくので好きにして頂戴。Wallis は、70MByteもあって、ppblog に撥ねられちゃったので断念。残念。

「ウォリス一万尺」バージョンを置いときました。小数点以下３桁あたりをうろちょろしています。最終行を思う存分コピーしてください。パソコン固まっても知らないよ。自己責任。

添付ファイル： 1352026185_Machin.xlsx